基于延迟补偿的异步SGD算法

最近看到一篇解决并行框架下解决梯度异步更新问题的论文，这里做一个简单的介绍。

【1】DC-ASGD

首先让我们来看一看异步SGD是怎么更新参数的

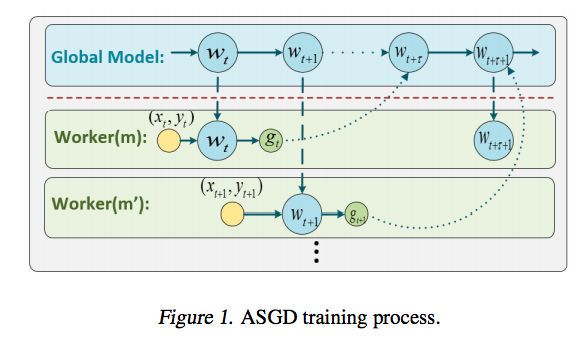
可见 $worker_{m}$ 从ps拉取的参数是 $w_{t}$ ，经过模型训练得到梯度 $g_{t}$ ，回传给ps的时候由于其他worker已经更新了参数，此时ps中参数$w$已经变成了$w_{t+\tau}$，回传的梯度$g _{t}$相比于参数$w_{t+\tau}$有了时间$\tau$的梯度延迟。在并行度较高的时候梯度延迟会导致较为严重的精度损失，模型收敛不如单线程更新。为解决异步梯度更新的问题，这篇论文采用了对当前梯度进行补偿的方法，旨在提升异步更新的模型收敛精度。

该论文借鉴了Folland, 2005将梯度 $g(\mathrm w_{t+\tau})$ 用泰勒展开成

$$g(\mathrm w_{t+\tau})=g(\mathrm w_{t})+\nabla g(\mathrm w_{t})(\mathrm w_{t+\tau}-\mathrm w_{t})$$

但是由于梯度的一阶微分对应的是原始损失函数$f$的二阶微分，这意味着必须要先计算Hessian矩阵，而Hessian矩阵的计算是非常耗时，尤其是变量维数较高的时候，有限的计算资源下几乎无法完成。因此作者采用一种近似公式替Hessian，最后得到参数向量$\mathrm w$的梯度更新式：

$$g(\mathrm w_{t+\tau})=g(\mathrm w_{t})+\lambda_{t} \cdot g(\mathrm w_{t}) \odot g(\mathrm w_{t}) \odot (\mathrm w_{t+\tau}-w_{t})$$

对应到单个参数$w$的更新式：

$$g(w_{t+\tau})=g( w_{t})+\lambda_{t} \cdot g(w_{t})\cdot g(w_{t}) \cdot (w_{t+\tau}-w_{t})$$

其中：

$$s_{t} = d \cdot s_{t-1} + (1-d) \cdot g(w_{t})$$ $$\lambda_{t} = \frac{\lambda_{0}}{\sqrt{s_{t} + \epsilon}}$$

注：$\epsilon$ 是一个很小的值，初始值避免除0；$\lambda _{0}$ 是超参，控制补偿的程度；$d$是衰减因子moving average步长； $s_{t}$ 是历史moving average衰减的梯度平方和。

因此ps端参数更新式为：

$$w_{t+\tau + 1} = w_{t+\tau} - \mu (\lambda_{t} \cdot g(w_{t})\cdot g(w_{t}) \cdot (w_{t+\tau}-w_{t}))$$

算法伪代码如下：

分为两部分ps端和worker端

worker端和普通基于ps的并行更新没有不同，ps端的运行机制分两种情况处理如下所示：

第一种是 $worker(m)$ 来拉取参数pull request，这时需要将当前的参数 $w_{t}$ 保存起来$w_{bak}(m)$

第二种情况是worker(m)回传梯度$g_{t}$，此时梯度将被补偿修正，然后用补偿修正后的梯度更新参数$w_{t+\tau}$

此种方法需要在ps端多存储$m+1$个参数：1. 历史moving average衰减的二阶梯度和 $s_{t}$ ，2.各个worker对应的备份参数 $w_{bak}(m)$ ，通常情况下这个额外的存储空间是可以接受的。

【2】改进版本

但是该实现方法有一点缺陷，通常worker的数量是动态调整的，假如实时数据量大涨，此时需要加大并行度这样一来ps端的 $w_{bak}(m)$ 的个数也需要动态增加，由于通常ps和worker是基于不同框架，逻辑修改较为繁琐。因此笔者对原来的算法稍加修改以最小限度的修改支持该算法。

修改后的算法伪代码如下：

改进版的ps不再为每个worker保存一份历史参数 $w_{bak}$ ，而是每次 worker 回传的时候随着梯度$g_{t}$ 的回传也将 $w_{t}$ 回传给ps，改动之后，适当增加了通信的开销，但是存储的空间花销降低了，且易于实现。

参考文献：

1. 文章作者talk视频
2. Asynchronous Stochastic Gradient Descent with Delay Compensation
3. Folland,Higher-order derivatives and taylor’s formula in several variables
4. 参考博文